지수의 계산 문의 드립니다.
2013.08.02 00:49
지수 계산에서 이해가 안되는 부분이 있어 문의 드립니다.
1번이 맞다는데 그 이유가 무엇인가요?
그럼 2번의 답이 -9가 되는데 1번이 맞다는 전제하에 2번은 이해가 됩니다.
그러면 3번의 답은요? -27이 맞는지요? 아니면 27i 가 맞는지요?
코멘트 6
-
김군
08.02 07:30
-
기둥
08.02 08:25
상세하고 친절한 답변 고맙습니다.
1번의 경우 홀수 제곱 했을 때 음수가 나오는 것은 음수이기 때문이라는 점이 핵심인 것 같습니다.
그럼 다음 질문이 떠오릅니다. 짝수 제곱해서 음수가 나온다면 즉
육제곱근 -5 는 어떻게 되는지요?
이 질문은 3번과도 연관이 있는데요. 이제곱해서 음수가 나올 수는 없기 때문에 허수 아이를 만들어 사용하지 않습니까? 이것은 이제곱일 때만 해당되는 것인가요? 아니면 짝수제곱에 모두 사용할 수 있는 것인가요?
-
꼬소
08.02 10:35
허수는 2 제곱에만 음수가 나옵니다..
4 제곱을 하면 양수로 나옵니다. (2 제곱이 음수이고 거기에 제곱을 하므로 양수가 됩니다.)
※ 제곱근의 값이 2일 경우를 가정하여 이야기 드린 것입니다.
-
기둥
08.02 11:09
아하. 좋은 힌트가 되었습니다. 이제곱근의 이제곱근으로 이어나갈 수가 있군요. 그러면 ...
-
왕초보
08.03 07:18
순허수가 그렇고요.. 복소수는 얘기가 조금 다르죠. ( ..)
-
꼬소
08.03 19:14
ㄷㄷㄷㄷㄷㄷ 제곱근만 한정 해요 우리......

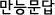
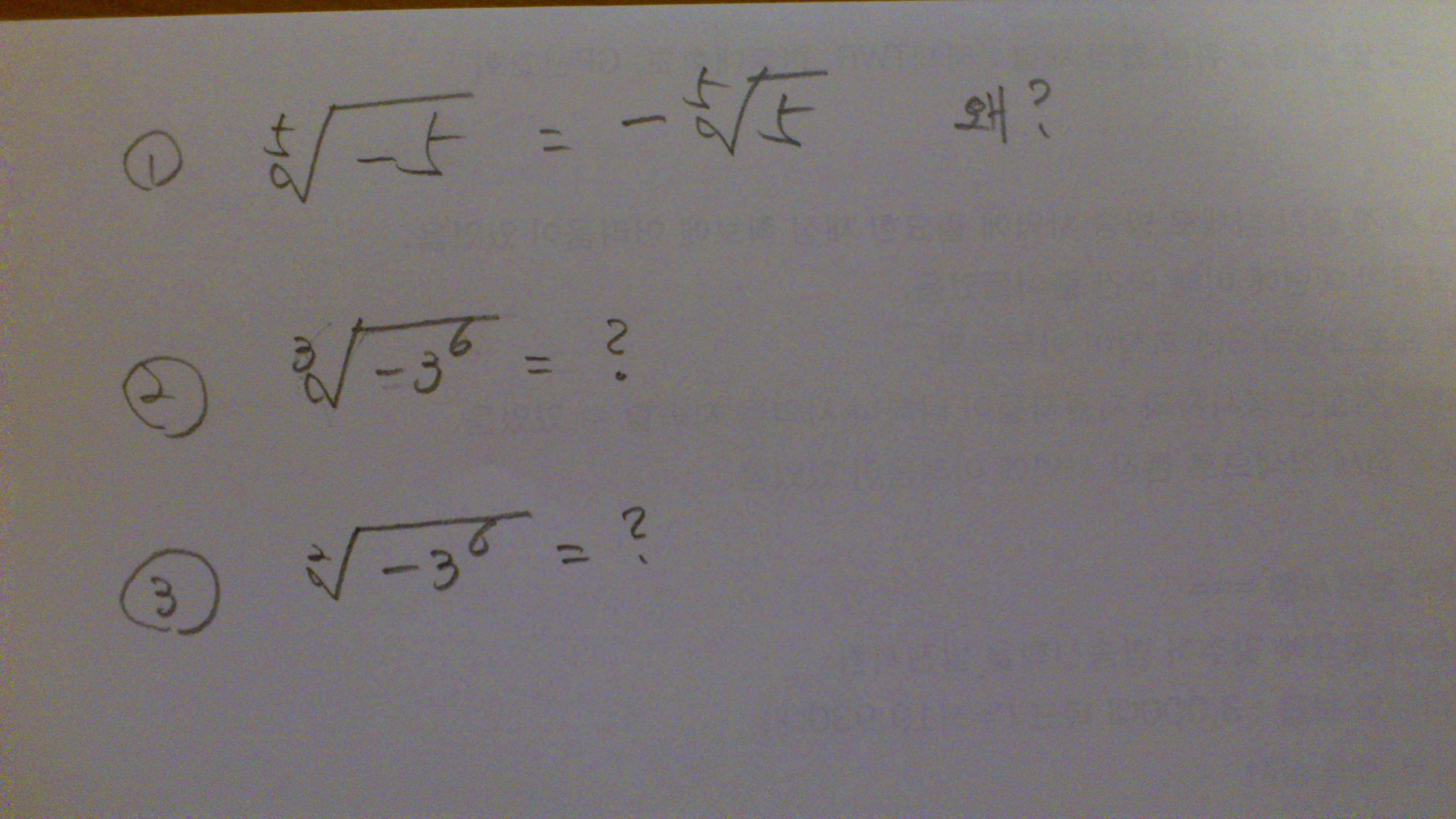
1번은 다섯제곱했을 때 -5가 되는 값을 찾는 것입니다. 그 값이 뭔지 몰라도 -5와 같이 음수겠죠? 왜냐하면 다섯제곱은 원래 수의 부호를 그대로 보존하니까요: (-1)^5=-1, (-2)^5=-32, (-3)^5=-273, 이런 식이죠. 일반적으로 말해서, k가 양의 홀수일때, n^k<0이면 n<0입니다. 이것은 k가 양의 홀수일 때, n>=0이면 n^k>=0이기 때문이죠.
그리고 2번 문제는 괄호를 써줘야 하는데, 출제자가 조심스럽지 못하네요. (-3)^6의 세제곱근은 +9인 반면 -(3^6)의 세제곱근은 -9입니다. 이것은 위에 이미 설명한 대로 세제곱근은 부호를 보존하는 연산이기 때문이죠.
3번 문제 역시 괄호가 중요한 경우입니다. (-3)^6은 3^6과 같고 그 제곱근은 +27과 -27 둘인데 대개 양수의 제곱근을 찾으라고 할 때에는 양의 제곱근을 찾으란 거니까 +27이 될 거고요. -(3^6)의 제곱근은 허수인 27i밖에 없는 거죠.
그럼 답이 뭐란 거냐... 문제가 개떡같아서 유일하게 맞는 답이 없다는 것인데, 2번 문제의 정답이 -9로 나와있다면 ^을 -보다 먼저 적용하겠다는 거니까 (즉 -n^k라면 -(n^k)로 이해하겠다는 얘기니까) 3번 문제의 경우에도 -(3^6)의 제곱근을 찾으란 얘기일 거고, 27i가 되겠죠. 출제자가 일관성있는 표기법을 사용하고 있다는 전제 하에 그렇다는 거지만요.