수학-명제와 증명에서
2010.11.03 15:21
아들 녀석 수학을 봐주고 있습니다.
명제와 증명에서 아래와 같은 문제가 나왔습니다.
명제 p의 집합을 집한 P, q의 집합을 집합 Q, r의 집합을 집합 R이라고 할 때,
p->q와 q->r이 모두 참 일 때 다음 중 맞는 것은?
1) P( Q : 기호가 표기 안되서 그러는데요. 집합 P는 집합 Q의 부분 집합이다.
...
...
그런데, 해설집을 보니
p -> q 가 참이면 집합 P는 집합 Q의 부분 집합이다. 라고 설명이 되어 있습니다.
이게 왜 그런가요?
코멘트 4
-
유년시절
11.03 15:46
-
유년시절
11.03 15:47
아참, p -> q = ~p or q의 증명은 진리표를 그려 진리값을 따져서 진리값이 같음을 증명하면 됩니다.
-
왕초보
11.04 01:11
저거 정의에서 바로 증명될 겁니다.
집합P가 Q의 부분집합이라는 것의 정의가..
P의 원소인 모든 p가 Q의 원소이기도 하면 P를 Q의 부분집합이라고 한다.. 이고..
p->q가 참이라는 얘기가 바로 저 정의라서.. -_-;;
-
즐거운하루
11.05 13:45
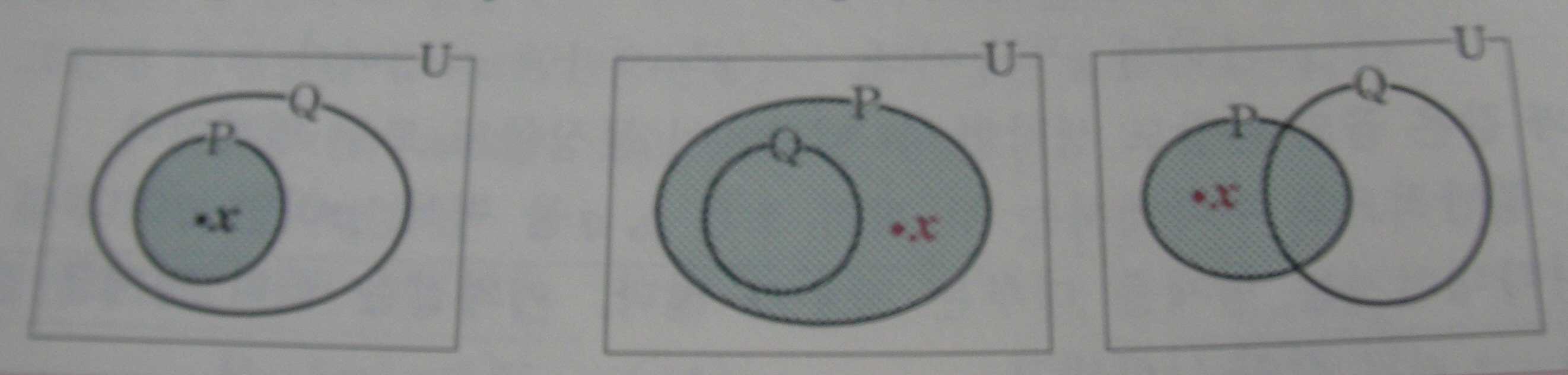
벤다이어그램을 보시면 1번인경우(p가 q의 부분집합인경우)는 반례가 생기지 않지만
2번 3번의 경우 원소 x를 보시면 p의 원소라고 해서 q의 원소가 아닌경우가 생기므로
"p이면 q이다"가 참이 아니게 됩니다.
따라서 "p이면 q이다"가 참이려면 1번의 경우밖에 해당되지 않네요.
"p이면 q이다" 를 말 그대로 해석하면 p인경우 반드시 q가 되냐? 뭐 이런얘기입니다.
글로 설명하기 힘드네요.^^

p -> q = ~p or q 쟎아요.
이는 P^ ∪ Q의 합집합은 전체 집합임을 의미하고요.(여집합을 의미하는 윗첨자 c를 표현할 수 없어 ^를 대체하여 사용했습니다.)
그러면 P ⊆ Q일 수 밖에 없죠.